Matplotlib Homework
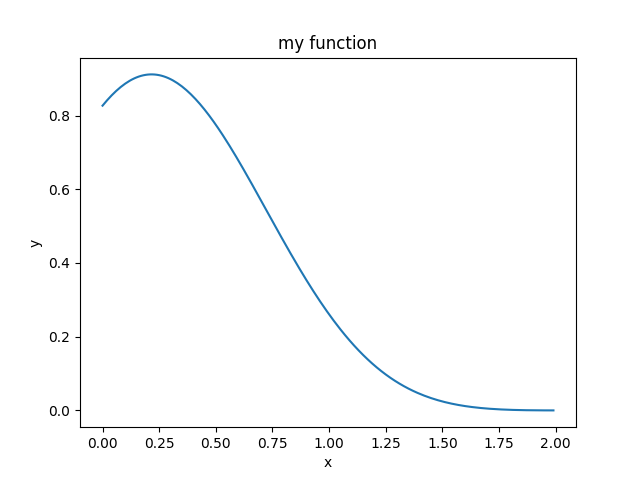
Exercise 11.1: Plotting a function
Plot the function $f(x)=\sin^2(x-2)e^{-x^2}$ over the interval [0, 2]. Add proper axis labels, a title, etc.
使用matplotlib即可画出图像。
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(0, 2, 0.01)
m1 = np.sin(x-2) ** 2
m2 = np.exp(- x ** 2)
y = m1 * m2
fig, ax = plt.subplots()
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('my function')
plt.show()
其中np.arange(0, 2, 0.01)产生等分的小区间。其返回值是一个np.array
m1和m2分别是表达式的两个因子。y可表示成他们的乘积。
在求出x和y后,利用plt.plot(x, y)将图像画出。需要留意,最后必须用plt.show(),否则图像无法显示。
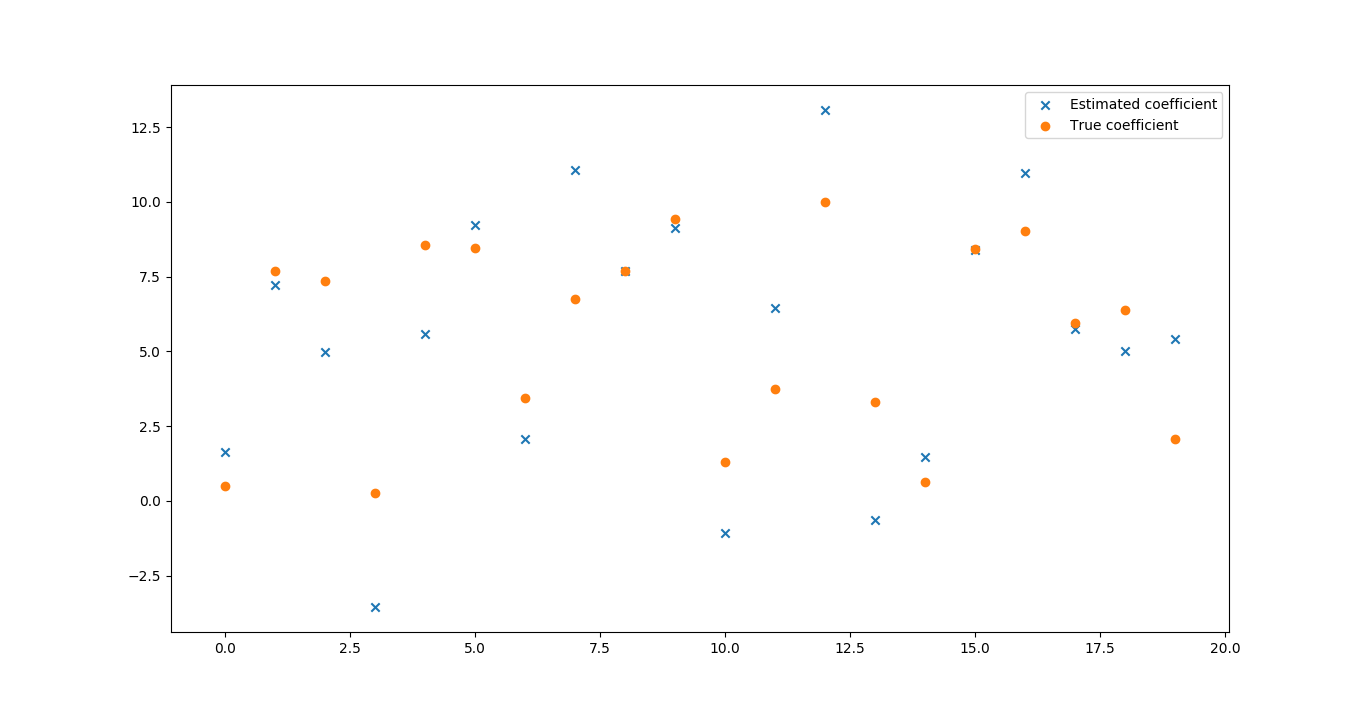
Exercise 11.2: Data
Create a data matrix X with 20 observations of 10 variables. Generate a vector b with parameters Then generate the response vector y = Xb+z where z is a vector with standard normally distributed variables. Now (by only using y and X), find an estimator for b, by solving $\hat b = \arg \min_b \big | \big | Xb-y \big | \big |_2$ Plot the true parameters b and estimated parameters b̂. See Figure 1 for an example plot.
import numpy as np
ROW = 30
COL = 20
SCALE = 10
X = SCALE * np.random.random((ROW, COL))
b = SCALE * np.random.random(COL)
print(b)
b.shape = (COL, 1)
mu, sigma = 0, 1
z = np.random.normal(mu, sigma, ROW)
z.shape = (ROW, 1)
y = X.dot(b) + z
from numpy.linalg import inv
est = np.dot(
inv(np.dot(X.transpose(), X))
, np.dot(X.transpose(), y)
)
print(est)
import matplotlib.pyplot as plt
x = [i for i in range(COL)]
plt.subplots()
plt.scatter(x, est.tolist(), marker='x', label='Estimated coefficient')
plt.scatter(x, b.tolist(), marker='o', label='True coefficient')
plt.legend()
plt.show()
代码大体分为3个部分。第一个部分用于产生随机的矩阵和向量。这些函数的用法在前面的博客中已经提到过。
第二部分计算估计值est
利用公式
将其翻译成numpy的代码即可。
第三部分是画图。由于本题要画散点,故使用plt.scatter函数作图。其用法与plt.plot类似。
marker关键字用于指定在图片中显示的符号。label用于显示右上角的legend。要显示legend,最后必须有plt.legend(),否则不会显示。`
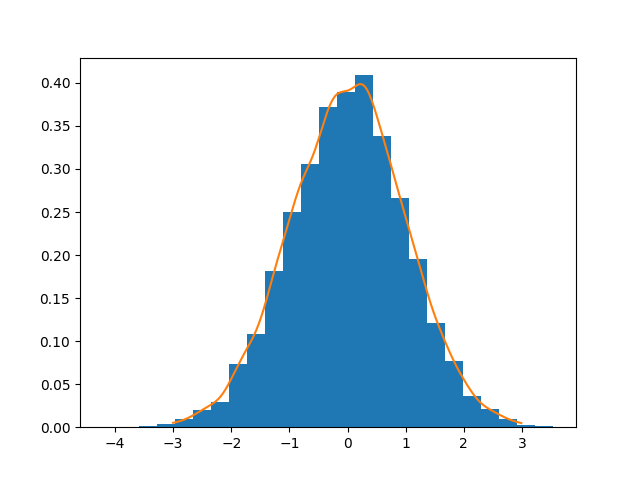
Exercise 11.3: Histogram and density estimation
Generate a vector z of 10000 observations from your favorite exotic distribution. Then make a plot that shows a histogram of z (with 25 bins), along with an estimate for the density, using a Gaussian kernel density estimator (see scipy.stats). See Figure 2 for an example plot.
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
mu, sigma = 0, 1
x = np.random.normal(mu, sigma, 10000)
plt.hist(x, 25, normed=True)
kernel = stats.gaussian_kde(x)
sample_x = np.arange(-3, 3, 0.01)
xs = kernel.evaluate(sample_x)
print(xs)
print(np.sum(xs))
plt.plot(sample_x, xs)
plt.show()
本题在产生随机的高斯分布后,使用plt.hist函数产生柱形图。
plt.hist(x, 25, normed=True)
第一个参数传递进数据集。第二个参数传递分成的组(bins)的个数。第三个参数设置normed为True,会对数据结果作规范化。
kernel = stats.gaussian_kde(x)
xs = kernel.evaluate(sample_x)
上述代码的第一行使用scipy.stats.gaussion_kde工具来估计概率密度。传入的参数是数据集。
kernel.evaluate对输入的x,计算其相应位置的概率密度。
随后的plt.plot函数把概率密度曲线画出来。
可以看到,在数据量较大(10000)时,柱状体和曲线大致是一致的。